Necessary Conditions for Deadlock:
In a multiprogramming environment, several processes may compete for a finite number of resources. A process requests resources and if the resources are not available at that time, the process entries awaiting stability. It may happen that the waiting process will never again change state because the resources, it has requested are held by other waiting processes. This situation is called a deadlock. Let us consider a system with three tape drives and there are three processes each holding one of these tape drives. If each process now requests another tape drive, the three processes will be in a deadlock state. In the rest of this article, we are going to discuss the Necessary Conditions for Deadlock, Resource-allocation Graph in Deadlock, and Methods for Handling Deadlock.
Necessary Conditions for Deadlock:
A deadlock situation can arise if the following four conditions hold simultaneously in a system:
- Mutual Exclusion: at least one resource must behold in a non-shareable mode; that is only one process at a time can use the resource. If another process requests that resource, the requesting process must be delayed until the resource has been released.
- Hold and Wait: A process must be holding at least one resource and waiting to acquire additional resources that are currently being held by other processes.
- No Preemption: Resources can’t be preempted; that is, a resource can be released only voluntarily by the process holding it, often that process has completed its task.
- Circular wait: A set {P0, P1, P2, – – – – -, Pn} of waiting process must exist such that P0 is waiting for a resource held by P1. P1 is waiting for a resource held by P2, – – – – – Pn-1 is waiting for a resource held by Pn and Pn is waiting for a resource held by P0.
These four Necessary Conditions for Deadlock are arising simultaneously in a system.
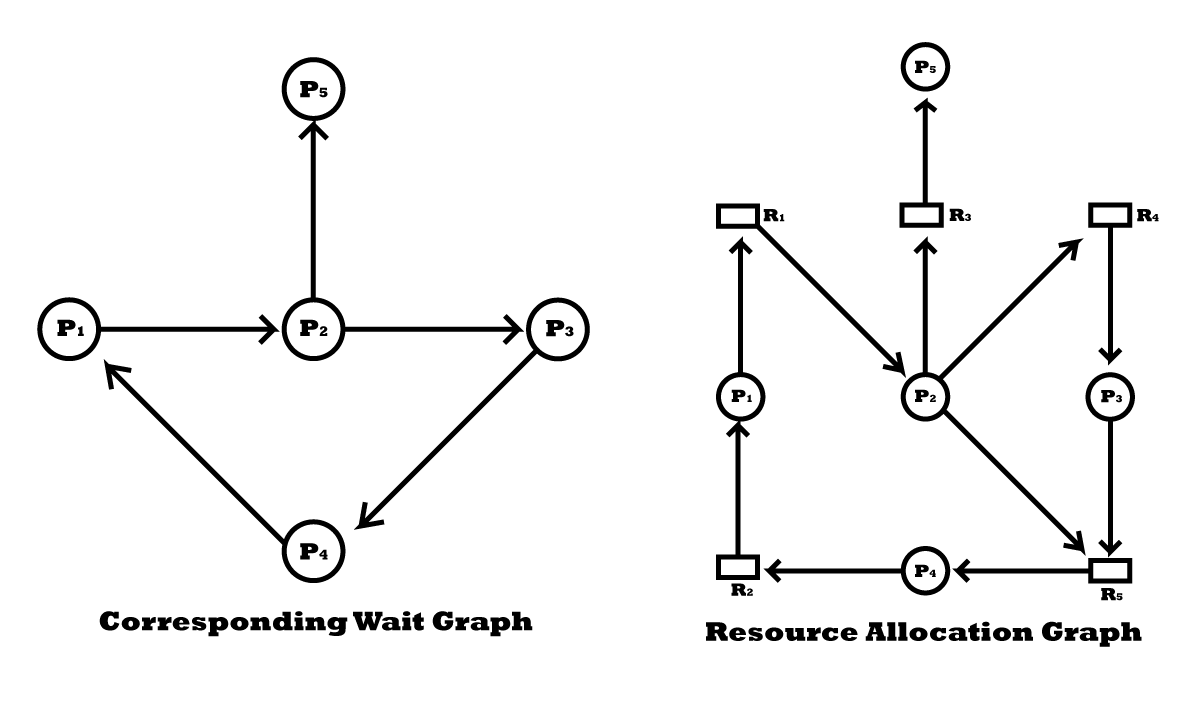
Resource-allocation Graph in Deadlock:
A resource-allocation group can be used to describe deadlocks precisely. This group consists of a set of vertices V and a set of edges E. The set of vertices V is partitioned into two different types of nodes P = {P1, P2, – – – – -, Pn}, the set of consisting of all the active processes in the system and R = {R1, R2, – – – – -, Rn}, the set consisting of all resources types in the system.
A directed edge from process Pi to resource type Rj (denoted by Pi → Rj) signifies that process pi has requested an instance of resource type Rj and is currently waiting for that resource. A directed edge Pi → Rj is called a request edge.
A directed edge from resource type Rj to process Pi (denoted by Ri → Pj) signifies that an instance of resource type Rj has been allocated to process Pi. A directed edge Ri → Pj is called an assignment edge. Pictorially, each process is represented by a circle and each resource is represented by a square.
It can be shown that if the graph contains no cycles, then no process in the system is deadlocked. On the other hand, if the graph contains a cycle, then a deadlock may exist. If each resource type has exactly one instance, then a cycle implies that a deadlock occurred. If each resource type has several instances, then a cycle does not necessarily imply that a deadlock occurred.
Let us consider the resource-allocation graph shown in the following figure:
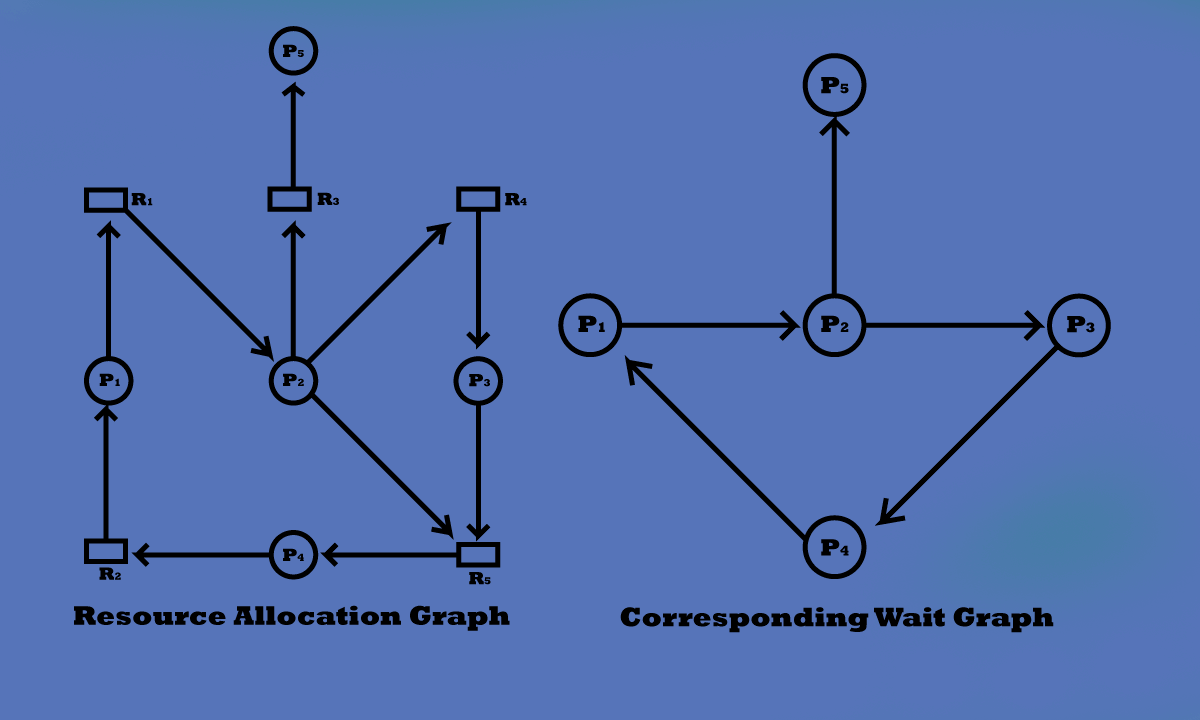
Two minimal cycles exist in the system:
P1→ R1→ P2→ R3→ P3→ R2→ P1
P2→ R3→ P3→ R2→ P2
Here, processes P1, P2, and P3 are deadlock. Process P2 is waiting for the resource R3, which is held by process P3. Process P3 is waiting for either P1 or process P2 to release resource R2. In addition, process P1 is waiting for process P2 to release resource R1.
Methods for Handling Deadlock:
There are three methods to deal with the deadlock problem. They are given below:
i. We can use a protocol to prevent or avoid deadlocks, ensuring that the system will never enter a deadlock state.
ii. We can allow the system to enter a deadlock state, detect it, and recover.
iii. We can ignore the problem altogether and pretend that deadlocks never occur in the system.
Reference: Operating System Concepts written by Abraham Silberschatz, Peter Baer Galvin, and Greg Gagne.

Library Lecturer at Nurul Amin Degree College